Point cloud 기반의 learning에는 VoxelNet과 같은 grid 기반의 방법, PointNet과 같은 mlp 기반의 방법 등 다양한 방법이 있습니다. 그중에서도 2D domain에서 큰 성능을 보인 CNN을 point cloud에 직접 적용하기 위해 PointwiseCNN1, SpiderCNN2, PCNN3 등 다양한 방법들이 발전해왔습니다. KPConv는 이처럼 point cloud를 변환 없이 그대로 conovlution을 적용할 수 있도록 하는 방법으로 ICCV 2019에서 발표된 논문입니다.
1. Kernel point convolution
KPConv는 그림과 같이 기존 이미지 convolution과 유사하게 적용됩니다. 기존 2D image와 같이 각 point(이미지에서는 pixel)가 $D_{in}$개의 feature channel이 있을 때 $D_{out}$개의 kernel이 적용되어 $D_{out}$개의 feature channel이 생성됩니다.

KPConv는 정해진 격자 kernel이 아닌 일정한 반지를 r을 가지는 구 형태의 kernel을 가집니다. 구 형태의 kernel 안에는 기존 convolution kern의 grid 역할을 하는 kernel point가 있어 이를 이용해 convolution을 수행합니다. 이때 논문의 저자는 KNN보다 정해진 r값을 이용하는 것이 point의 density에 robust 하고, 일정한 구 형태의 domain이 network가 의미 있는 representation을 학습하는데 도움이 된다고 이야기했습니다.
kernel 속 kernel point는 정해진 위치에 각각의 weight를 가지고 존재합니다. 이 kernel point weight가 input point feature와 곱해지며 새로운 feature를 생성하는 것은 기존의 convolution과 동일하지만 point는 continuous 하기 때문에(kernel point의 위치가 input point와 같은 위치에 있는 것은 거의 불가능하기 때문에) input point가 어떤 kernel point의 weight를 이용할지 결정하는 것이 중요합니다. KPConv는 하나의 point feature가 모든 kernel point weight와 계산된 뒤 합해져서 새로운 feature를 생성합니다. 계산 식은 아래와 같습니다.


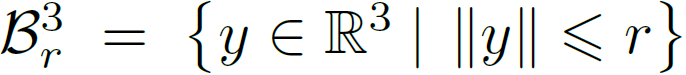
convolution kernel function $g$와 correlation 함수 $h$는 다음과 같습니다. $h$는 $\tilde{x}_k$와 $y_i$의 correlation으로 서로 가까울수록 높은 값을 가지게 됩니다.


식에서 볼 수 있듯이 input point $x_i$의 상대 좌표($y_i$)와 kernel point의 좌표를 이용해 거리에 linear 하게 비례하는 correlation $h$가 계산됩니다. 이 $h$값과 weight가 곱해져 같은 kernel point와 계산되더라도 그 거리에 따라 크기가 결정됩니다. 이 방법으로 모든 point들의 feature값이 계산되면 기존 convolution과 같이 모두 합하여 center point의 feature가 됩니다.
이를 이해하기 쉽게 2D로 보면 각각의 kernel point는 파란 기둥 크기의 각각의 weight를 가지고 각 kernel point들 사이에 linear correlation 하게 weight값이 계산되어 kernel 내의 모든 영역에서 weight가 계산됩니다.

이렇게 정해진 kernel이 실제 point 배치와 만나게 된다면 weight가 높은 곳에 point가 가까울수록 큰 feature값을 가지게 됩니다. 아래 이미지를 보면 5 모양의 point 배치 중 직선과 같은 부분의 point가 큰 feature값을 가지는 것을 볼 수 있습니다.

KPConv는 이 kernel point가 고정된 rigid KPConv와 input point에 따라 kernel point의 위치가 변화하는 deformable KPConv 두 가지를 제안하였습니다. Rigid KPConv는 비교적 간단한 task인 classification, small segmentation task에 좋은 성능을 보였고, deformable KPConv는 많은 instance와 큰 다양성을 가지는 대규모 segmentation과 같은 복잡한 task에 좋은 성능을 보였다고 합니다.
Rigid KPConv

먼저 적절한 kernel point의 위치를 구하기 위해 kernel point 간의 거리가 멀수록 작아지는 repulsive petential과 구의 중심에서 kernel point가 무한히 멀어지는 것을 막기 위해 중심에서 가까울수록 작아지는 attractive potential을 정의하고 이 두 값의 합을 최소화하는 point 개수($K$) 별 배치를 구하였습니다. 그 결과 위와 같은 정다면체 형태의 배치가 가장 적절하다는 것을 증명하였습니다. 이후 Network에서 각 layer마다 정해진 kernel point 배치는 고정되고 적절한 radius값으로의 변경과 random 한 회전만을 적용한 point 배치를 사용하였습니다.
Deformable KPConv

기존 2D 이미지에서 좋은 효과를 보였던 deformable convolution을 point cloud에도 적용하였습니다. 정해진 위치의 kernel point를 사용하는 대신 kernel point의 위치를 적절하게 이동시킬 수 있다면 receptive field를 적절한 형태로 조절할 수 있습니다. 이를 위해 deformable KPConv는 Rigid KPConv의 결과로 K개의 kernel point의 변위를 구합니다. 이때 x, y, z 각 축으로의 변위가 필요하니 총 3K 개의 값이 구해지게 됩니다. 이후 이 변위 값이 적용된 kernel point를 이용해 convolution을 수행하게 됩니다.
그러나 이 방법은 point cloud의 sparsity 한 특성 때문에 드대로 적용할 수 없습니다. 이동된 kernel point 주변에 input point가 없다면 이 kernel point가 사용되지 않으므로 gradient가 null이 되어 point가 사라지게 됩니다. 실제로 저자는 네트워크가 수렴한 뒤 kernel point를 조사했을 때 종종 input point들에서 멀어져 빈 공간에 자리 잡는 것을 확인할 수 있었다고 합니다. 이 문제를 해결하기 위해 다음 두 regularization을 사용하였습니다.
- Fitting regularization : Kernel point와 거기서 가장 가까운 neighbor와의 거리를 이용. 서로 가까울수록 작은 값을 가짐

- Repulsive regularization : Kernel point 간의 거리가 멀수록 작은 값을 가짐. kernel point들이 같이 잘못된 위치에 빠지지 않도록 하는 역할을 함

그 결과 아래와 같이 고정된 위치에서 평평한 바닥에 적절하게 배치가 변형된 것을 확인할 수 있습니다.

2. Network

제안한 KPConv를 이용해서 KP-FCNN이라는 segmentation network와 KP-CNN이라는 classification network를 만들었습니다. Network의 각각의 layer에서는 grid dsubsampling을 수행하여 grid 내부의 무게중심 point만을 sampling 하여 downsampling을 수행합니다. 이 grid의 cell size는 2배씩 커지며 KPConv의 receptive field를 점점 증가시키게 됩니다. 새롭게 sampling 된 point들의 feature는 image strided convolution과 유사한 strided KP-Conv를 사용하여 pooling 합니다.
이처럼 이미지와 같이 pooling 되며 point의 개수는 줄어들고 channel size는 증가한 뒤 KP-CNN은 classification task를 수행하기 위해 fully conneted layer로 연결되어 classification을 수행합니다. 반면에 segmentation task를 수행하는 KP-FCNN은 nearest neighborhood 방법으로 U-Net 구조와 같이 다시 upsampling 되어 point 별 segmentation 결과를 얻게 됩니다.
두 네트워크 모두 classification과 segmentation task에서 SOTA를 달성하며 좋은 결과를 보였습니다.
- Binh-Son Hua, Minh-Khoi Tran, and Sai-Kit Yeung. Pointwise convolutional neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 984–993, 2018. [본문으로]
- Xu, Yifan, et al. "Spidercnn: Deep learning on point sets with parameterized convolutional filters." Proceedings of the European Conference on Computer Vision (ECCV). 2018. [본문으로]
- Matan Atzmon, Haggai Maron, and Yaron Lipman. Point convolutional neural networks by extension operators. ACM Transactions on Graphics (TOG), 37(4):71, 2018. [본문으로]